Мнемонические правила

   "Кто и шутя и скоро пожелает(ъ) пи узнать, число уж(ъ) знает(ъ)". Помните это двустишие? Вроде бы бессмыслица. Так, да не совсем. Конечно, приведённый стишок очень далёк от подлинной поэзии. Но он и придуман совсем не для того, чтобы воздействовать на человеческие сердца. Напротив, назначение его весьма прозаическое, и тем не менее вполне возможно, что сей труд будет как бесконечная эстафета передаваться из поколения в поколение... Дело в том, что он позволяет легко, быстро и с очень большой точностью написать известное из геометрии число "пи", которое характеризует отношение длины любой окружности к ее диаметру.
   Действительно, если пользоваться старой орфографией, принятой до 1918 года, то оказывается, что число букв в каждом слове этого двустишия соответствует очередной цифре числа "пи": 3,1415926536.
   Попробуйте-ка запомнить число без подсказки! А наша подсказка при всей своей видимой нелепости легко запоминается и даёт ключ к запоминанию точной величины часто употребляемого математического понятия.
   Приём, которым мы воспользовались для запоминания числа "пи", называется мнемоническим правилом. Словарь даёт следующее определение мнемоники: "Мнемоника (от греческого mnemonika – искусство запоминания) – система различных приёмов, облегчающих запоминание и увеличивающих объём памяти путём образования искусственных ассоциаций".
   Простейшими мнемоническими правилами люди пользовались ещё в глубокой древности. Например, зарубки, которые они оставляли на дереве, помогали им ориентироваться в дремучем лесу. А мой вполне современный товарищ, прикалывая к ремешку часов скрепку, утверждает, что она помогает ему вспомнить и выполнить данное обещание (например, принести из дома какой-либо предмет).
   Вернёмся, однако, к математике. С числом "пи", кажется, всё ясно. Но вот в высшей математике, которую изучают в институтах, широко, пользуются понятием другого числа e. Что это такое? В школе вас знакомят с десятичными логарифмами, основанием которых служит число 10. А существуют ещё и так называемые натуральные логарифмы. Так вот это число e и является основанием натурального логарифма. Его приблизительное значение 2,7. А точное выражается бесконечной десятичной дробью, которую, оказывается, очень легко запомнить вплоть до 15-го знака после запятой, если воспользоваться мнемоническим правилом:

e = 2,718281828459045.

   Присмотритесь, пожалуйста, внимательнее к написанному числу. Нетрудно заметить, что после цифры 7 дважды повторяются числа 1828, а их легко запомнить как год рождения Льва Николаевича Толстого. А затем идут числа, обозначающие углы прямоугольного равнобедренного треугольника: 45, 90, 45, – не правда ли? Вот вы и запомнили это громоздкое число задолго до поступления в институт, и, поверьте, уже на всю жизнь.
   Однако не станем увлекаться высшей математикой. Нам бы сейчас что-нибудь попроще. Допустим, мы с вами пока ещё только ученики 5–6-го классов, и нам никак не даётся умножение или деление положительных и отрицательных чисел – всё время путаемся в знаках: умножая, скажем, –5 на –3, мы получаем в ответе –15, а при делении + 20 на –4 получаем +5, за что учительница неизменно ставит нам 2 без всяких знаков.
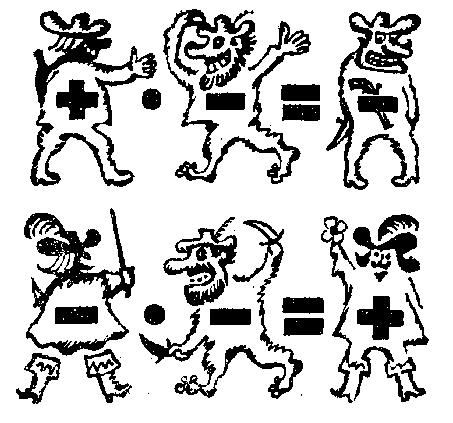   Помоги нам, добрая волшебница Мнемоника! И она помогает. Слушайте, ребята, и запоминайте.
   Положительный человек – это "+", и он, конечно, ваш друг.
   Отрицательный человек – это "–", он, безусловно, враг. Верно ведь? А теперь обратимся к арифметическим действиям:

1. ( + ) • ( + ) = ( + )
друг вашего друга – ваш друг

2. ( + ) • (-) = (-)
друг вашего врага – ваш враг

3. (-) • (+) = (-)
враг вашего друга – тоже ваш враг

4. (-) • (-) = ( + )
враг вашего врага – ваш друг.

   При делении – всё то же самое.
   Можно было бы продолжить подобные примеры. Но разве мнемонические правила – это привилегия математики? Ничего подобного. Вот, пожалуйста, известный пример из области физики. При прохождении белого света через призму наблюдается разложение его на цветной спектр, причём цвета в спектре располагаются всегда в строго определённом порядке: красный, оранжевый, жёлтый, зелёный, голубой, синий, фиолетовый.
   Уверяю вас, что запомнить эту последовательность, тем более надолго, было бы весьма сложно, если бы не одна "мудрая" фраза: "Каждый охотник желает знать, где сидит фазан".
   Первые буквы каждого слова этой фразы подсказывают нам нужный цвет.
   А если мы хотим быстро, не задумываясь представить семь цветов радуги в обратном порядке? И на это есть свой ключ – фраза, которая как бы отвечает на желание охотника: "Фазан сидит, глаза закрыв, желая очень кушать".
   Ну хорошо: математика и физика – науки точные. Может быть, в этом всё дело? Может быть, только поэтому мы и находим соответствующие закономерности даже в самом механизме запоминания? Однако если это так, то как же тогда быть с такой фразой: "Цыган на цыпочках стоит и "цыц" цыплёнку говорит"?
   Вы, наверное, уже догадались, что это – тоже мнемоническое правило. Никакого отношения к точным наукам оно не имеет. Им пользуются для запоминания следующего правила русской орфографии: после буквы Ц в корне пишется И, за исключением четырёх слов, перечисленных в приведённом выше двустишии: цыган, на цыпочках, цыц, цыплёнок.
   Или уж совсем короткая и ёмкая фраза: "Уж замуж невтерпёж", все три слова которой являются исключениями из другого правила подобного же рода: наречия, оканчивающиеся на шипящую, имеют на конце ь.
   А разве в быту, в повседневной жизни нам не помогает эта всемогущая мнемоника? Предположим, требуется запомнить номер телефона. Мы ищем какую-либо закономерность, пытаемся найти привычные ассоциации, и обычно находим.
   Мнемонику иногда обвиняют в том, что она приучает к чисто механическому запоминанию, без понимания сущности явления. Но ведь одно ни в коем случае не отрицает другого. Безусловно, изучая любой вопрос, нужно прежде всего понять его, осмыслить, прочувствовать. Но одно дело понять, а другое запомнить. Это разные вещи.
   Вы можете прекрасно понимать физическую сущность, скажем, того же числа "пи", знать, как оно получается, но не будете же вы каждый раз выводить его заново или искать значение этого числа в справочнике. Вам надо запомнить его. А как запомнить набор многих цифр? Вызубрить? Право, это весьма неблагодарная работа. И только мнемоника будет вам в этом случае надёжным и верным другом.
   Пусть закономерность, которую вы наблюдаете, используя мнемонические правила, чисто внешняя, не открывающая и не объясняющая окружающий вас мир, но она помогает усвоить многие его законы – усвоить их быстро и надолго. И я уверен, что каждый из вас в состоянии не только пользоваться известными мнемоническими правилами, но и сам придумывать новые.